Associativity and Precedence
Associativity and Operator Precedence are fundamental concepts in programming languages that define how expressions are evaluated. They determine the order of execution when multiple operators appear in an expression.
1. Associativity
Associativity defines how operators of the same precedence are grouped in the absence of parentheses. It determines the direction in which an expression is evaluated.
1.1 Types of Associativity
- Left-Associative Operators: Operators that group from left to right.
- Right-Associative Operators: Operators that group from right to left.
- Non-Associative Operators: Operators that cannot be chained together.
1.2 Left-Associativity
Most arithmetic and bitwise operators in C, Java, and Python are left-associative.
a - b - c // Evaluates as: (a - b) - c
x / y / z // Evaluates as: (x / y) / z
1.3 Right-Associativity
Some operators, such as assignment (=), exponentiation (** in Python), and ternary (?: in C/C++), are right-associative.
a = b = c // Evaluates as: a = (b = c)
x y z // Evaluates as: x (y z)
1.4 Non-Associative Operators
Relational operators such as <, >, == are non-associative because chaining them leads to ambiguity.
a < b < c // Invalid in C (Logical Error)
2. Operator Precedence
Precedence determines the order of execution when an expression contains multiple operators of different types.
2.1 Precedence Rules
- Operators with higher precedence are executed first.
- If operators have the same precedence, associativity decides the evaluation order.
- Parentheses
()override precedence rules.
2.2 Precedence Hierarchy (Common Programming Languages)
| Precedence Level | Operators | Associativity |
|---|---|---|
| 1 (Highest) | (), [], ->, . |
Left |
| 2 | ++, --, + (Unary), - (Unary), !, ~ |
Right |
| 3 | *, /, % |
Left |
| 4 | +, - |
Left |
| 5 | <<, >> |
Left |
| 6 | <, <=, >, >= |
Left |
| 7 | ==, != |
Left |
| 8 | & |
Left |
| 9 | ^ |
Left |
| 10 | | |
Left |
| 11 | && |
Left |
| 12 | || |
Left |
| 13 | ?: (Ternary) |
Right |
| 14 | =, +=, -=, *=, /= |
Right |
| 15 (Lowest) | , (Comma Operator) |
Left |
2.3 Example: Precedence in Arithmetic Expressions
Consider the expression:
id + id * id
Since multiplication (*) has higher precedence than addition (+), this is evaluated as:
id + (id * id)
2.4 Example: Overriding Precedence with Parentheses
By using parentheses, we can force addition to be executed first:
(id + id) * id
2.5 Example: Effect of Associativity
Given:
100 / 5 * 2
Since division (/) and multiplication (*) have the same precedence, and they are left-associative, this is evaluated as:
(100 / 5) * 2 // Output: 40
3. Real-World Applications of Associativity & Precedence
- Compilers (GCC, Clang, Java Compiler): Implement precedence parsing to generate correct syntax trees.
- Mathematical Computation Tools (MATLAB, Wolfram Alpha): Use precedence rules for expression evaluation.
- Database Systems (SQL Query Optimizers): Parse expressions based on operator precedence.
- Programming Language Design: Languages like Python and JavaScript handle associativity & precedence in interpreters.
4. Visualizing Operator Precedence in Parse Trees
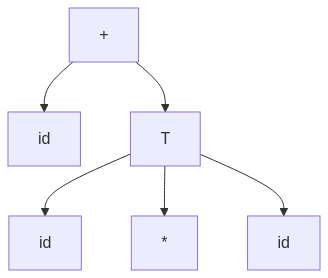
4.1 Example: Parse Tree for id + id * id
graph TD;
E["\+"] --> id1["id"];
E["\+"] --> T["T"];
T["T"] --> F1["id"];
T["T"] --> Op["\*"];
T["T"] --> F2["id"];
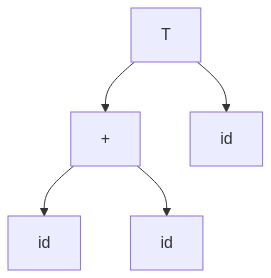
4.2 Example: Parse Tree for (id + id) * id
graph TD;
T["T"] --> E["+"] --> id1["id"];
E["+"] --> id2["id"];
T["T"] --> F["id"];
5. Summary
| Concept | Description | Example |
|---|---|---|
| Associativity | Defines order of execution for operators of equal precedence. | a - b - c → (a - b) - c |
| Precedence | Defines which operator executes first when multiple operators appear. | a + b * c → a + (b * c) |
| Left-Associative Operators | Evaluated left to right. | a / b / c → (a / b) / c |
| Right-Associative Operators | Evaluated right to left. | a = b = c → a = (b = c) |
| Non-Associative Operators | Cannot be chained. | a < b < c (Invalid in C) |