1. Parse Trees

A parse tree is a hierarchical tree structure that represents how a string conforms to a given grammar. It is used in syntax analysis to check whether a given input string belongs to a language.

1.1 Properties of a Parse Tree

• Root: The topmost node represents the start symbol of the grammar.
• Leaves: The terminal symbols of the grammar appear at the leaves.
• Internal Nodes: Each internal node represents a nonterminal, which expands based on grammar rules.
• Children Order: If a nonterminal expands into a sequence of symbols, they appear as its children from left to right.
• Yield: The string obtained by reading all the leaves from left to right is called the yield or frontier of the parse tree.

2. Example 1: Arithmetic Expression Parsing

Given the following CFG for arithmetic expressions:

E → E + T | E - T | T
T → T * F | T / F | F
F → (E) | id
  

This grammar ensures that * and / have higher precedence than + and -, and that the operators + and - are left-associative.

2.1 Leftmost Derivation for id + id * id

We perform a step-by-step leftmost derivation, always replacing the leftmost nonterminal:

Step 1: Start with E

E
  

Step 2: Expand the leftmost E using E → E + T

E ⇒ E + T
  

Step 3: Replace the leftmost E (in E + T) using E → T

E + T ⇒ T + T
  

Step 4: Expand the leftmost T using T → F

T + T ⇒ F + T
  

Step 5: Replace F with an identifier (F → id)

F + T ⇒ id + T
  

Step 6: Expand the remaining T (after the +) using T → T * F

id + T ⇒ id + T * F
  

Step 7: Replace the leftmost T in T * F using T → F

id + T * F ⇒ id + F * F
  

Step 8: Replace each F with id (F → id)

id + F * F ⇒ id + id * F ⇒ id + id * id
  

This leftmost derivation confirms that multiplication is performed before addition.

2.2 Parse Tree Representation (Leftmost Derivation)

The parse tree visually captures the hierarchy of operations. Since multiplication has higher precedence than addition, the subtree for id * id is built first.

Step 1: Begin with the root node

Start with the start symbol E:

Step 2: Expand E → E + T

This expansion introduces the addition operator:

Step 3: Expand the left E as E → T and then T → F with F → id

This gives the left operand:

Step 4: Expand the right T using T → T * F

This introduces the multiplication operator for the right operand:

Step 5: Expand the left T in the multiplication to T → F with F → id

This gives the left operand of multiplication:

Step 6: Replace the right F with id

This gives the right operand of multiplication:

The complete parse tree confirms that id + id * id is grouped as id + (id * id), reflecting correct operator precedence.

2.3 Rightmost Derivation for id + id * id

In a rightmost derivation we always replace the rightmost nonterminal first:

Step 1: Start with E

E
  

Step 2: Expand the rightmost nonterminal in E using E → E + T

E ⇒ E + T
  

Step 3: Expand the rightmost nonterminal (now T) using T → T * F

E + T ⇒ E + T * F
  

Step 4: Replace the rightmost nonterminal (F) with id

E + T * F ⇒ E + T * id
  

Step 5: Expand the rightmost nonterminal in T * id (the T) using T → F

E + T * id ⇒ E + F * id
  

Step 6: Replace the rightmost nonterminal (F) with id

E + F * id ⇒ E + id * id
  

Step 7: Now, the only remaining nonterminal is the leftmost E in E + id * id. Replace it using E → T

E + id * id ⇒ T + id * id
  

Step 8: Expand the remaining T using T → F

T + id * id ⇒ F + id * id
  

Step 9: Replace F with id

F + id * id ⇒ id + id * id
  

This rightmost derivation also leads to the expression id + id * id, with the multiplication carried out before addition.

2.4 Parse Tree for Rightmost Derivation

The following parse tree illustrates the derivation when the rightmost nonterminal is replaced first:

Step 1: Start with the root node

Step 2: Expand E → E + T

Step 3: Expand the rightmost T using T → T * F

Step 4: Replace the rightmost F with id

Step 5: Expand T_mult using T → F and then F → id

Step 6: Finally, replace the remaining nonterminal in the left branch (E_left) by applying E → T, then T → F, and F → id

The complete parse tree again shows that the expression is parsed as id + (id * id), confirming the correct associativity and precedence.

Quick Recap

• Leftmost Derivation: Always replaces the leftmost nonterminal first.
• Rightmost Derivation: Always replaces the rightmost nonterminal first.
• Parse Trees: Both derivations lead to the same overall parse tree.
• Correct Associativity: The tree ensures that multiplication (with higher precedence) is performed before addition.

Summary of Arithmetic Expression Parsing

The parsing steps demonstrated above correctly follow the CFG:

E → E + T | E - T | T
T → T * F | T / F | F
F → (E) | id
  

The fact that both the leftmost and rightmost derivations yield the same final parse tree indicates that the grammar is unambiguous. Here, although there are different derivation orders (leftmost versus rightmost), they both lead to the same unique tree structure for the expression id + (id * id).

The parse tree derived in section 2.2 and 2.4 confirms that id + id * id is grouped as id + (id * id) — ensuring that multiplication is evaluated before addition.

Explanation:

• The root node E represents the entire expression.
• Since addition (+) has lower precedence than multiplication (*), the expression is parsed as id + (id * id).
• The subtree for id * id is evaluated first, reflecting the operator precedence.

3. Leftmost and Rightmost Derivations

A parse tree corresponds to both leftmost and rightmost derivations. These derivations determine the order in which nonterminals are expanded.

3.1 Leftmost Derivation

E → E + T
  → T + T
  → F + T
  → id + T
  → id + T * F
  → id + id * F
  → id + id * id

3.2 Rightmost Derivation

E → E + T
  → E + T * F
  → E + T * id
  → E + F * id
  → E + id * id
  → F + id * id
  → id + id * id

4. Example 2: Ambiguous Grammar

A grammar is ambiguous if there exists more than one valid parse tree for the same input string.

Consider this ambiguous grammar:

E → E + E | E * E | id

For the input string id + id * id, we get two possible parse trees:

4.1 Correct Parse Tree (Multiplication Precedence)

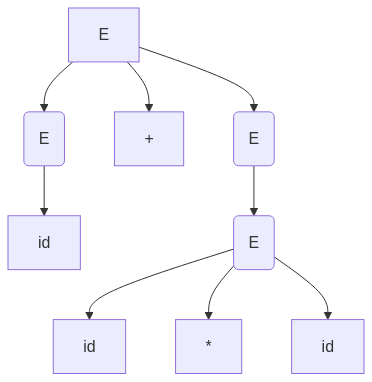
Step-by-Step Derivation (Correct Interpretation: Multiplication has higher precedence than addition)

We begin with the input string: id + id * id

1. Start with E:
   E → E + E   (Choose rule for addition)

2. Expand the second E (right operand of +) as multiplication has higher precedence:
   E → E + (E * E)  (Choose rule for multiplication first)

3. Expand the operands:
   E → id + (id * id)

4. Verify that multiplication is performed first due to its higher precedence.

Thus, the parse tree follows the correct operator precedence.

4.2 Incorrect Parse Tree (Addition Precedence)

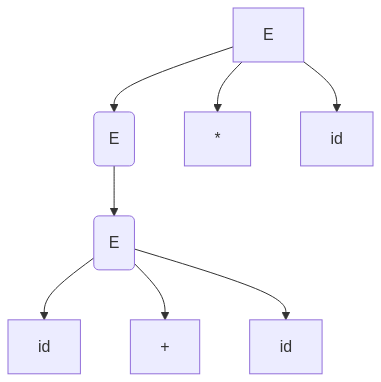
Step-by-Step Derivation (Incorrect Interpretation: Addition has higher precedence than multiplication)

We begin with the same input string: id + id * id

1. Start with E:
   E → E * E   (Incorrect choice of multiplication first)

2. Expand the left operand first:
   E → (E + E) * E   (Addition is handled before multiplication, which is wrong)

3. Expand operands:
   E → (id + id) * id

4. This results in incorrect evaluation since addition should not be performed before multiplication.

This parse tree incorrectly prioritizes addition over multiplication, violating standard arithmetic rules.

To remove this ambiguity, we modify the grammar to enforce operator precedence.

4.3 Resolving the Ambiguity

To enforce correct precedence, we modify the grammar:

E → E + T | T
T → T * F | F
F → id

Now, multiplication has higher precedence because:

• T handles * before passing results to E.
• E only processes + after resolving all * operations.

With this modification, we ensure that id + id * id is always parsed correctly as id + (id * id).

5. Example 3: Nested Expressions with Parentheses

Parentheses change the evaluation order of expressions. Consider the following grammar:

E → (E) | E + E | E * E | id

For the input (id + id) * id, the parse tree looks like:

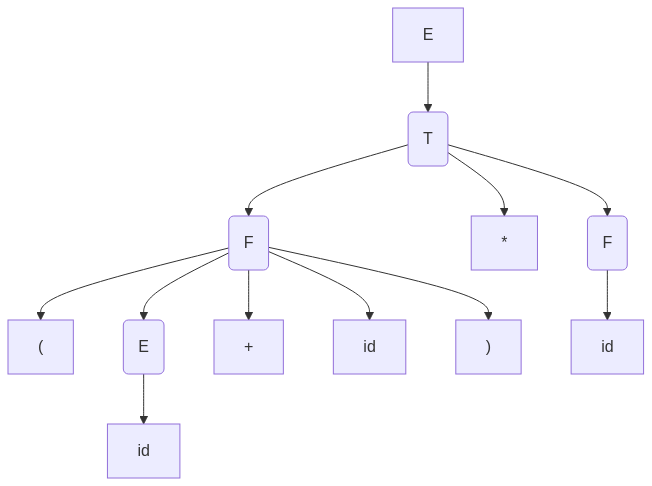
Explanation:

• Parentheses enforce that id + id is evaluated before multiplication.
• The subtree (id + id) is encapsulated inside F, ensuring correct precedence.

6. Constructing Parse Trees Using Code

We can use Python's nltk library to generate parse trees for a given grammar.

from nltk import CFG
from nltk.parse.chart import ChartParser

# Define a simple grammar
grammar = CFG.fromstring("""
    S -> NP VP
    NP -> 'John' | 'Mary' | 'dogs'
    VP -> V NP | V
    V -> 'barks' | 'sees'
""")

# Create a parser
parser = ChartParser(grammar)

# Parse the sentence
sentence = "John sees dogs".split()
for tree in parser.parse(sentence):
    print(tree)
    tree.pretty_print()

This code constructs a parse tree for the sentence "John sees dogs" based on the defined CFG.

7. Conclusion

Parse trees are essential for understanding the structure of expressions and programming languages. They provide a hierarchical view of syntax, guiding both parsing and code generation.

• Leftmost and Rightmost Derivations: Define how trees are built step-by-step.
• Ambiguity Resolution: Ensures a single unique parse tree exists for each input.
• Operator Precedence: Determines the order of operations.
• Practical Applications: Parsing in compilers, natural language processing, and query evaluation.