What is Syntax Analysis?
Syntax Analysis, also known as parsing, is the second phase of the compilation process. It takes the sequence of tokens generated by the lexical analyzer and organizes them into a structured format, typically represented as a parse tree or syntax tree.
The main goal of syntax analysis is to verify whether the sequence of tokens follows the grammatical rules of the programming language.
Key Function: Ensures that the program structure is valid before proceeding to further compilation phases.
Example of Syntax Analysis
Consider the following C statement:
int x = 10 + 5 * 2;After lexical analysis, it is converted into a sequence of tokens:
[int, identifier(x), =, number(10), +, number(5), *, number(2), ;]Syntax analysis checks whether this sequence conforms to the grammar of the language and generates a parse tree.
Why is Syntax Analysis Needed?
Syntax analysis plays a crucial role in ensuring that a program adheres to the correct structure defined by a language.
- Ensures Correct Syntax: Detects violations of language rules.
- Generates Structured Representation: Produces parse trees for further processing.
- Enables Meaningful Error Detection: Helps identify errors early in the compilation process.
- Provides Input to Semantic Analysis: The syntax tree is used in later stages for meaning verification and optimization.
Practical Scenario: Syntax vs. Semantic Errors
Consider the following Java code:
int a = 5 + ;This will result in a syntax error because a valid expression must follow the `+` operator.
However, the following code:
int a = 5 / 0;Has correct syntax but results in a semantic error (division by zero).
Components of Syntax Analysis
Syntax analysis consists of several key components that work together to process and validate the structure of a program.
- Context-Free Grammar (CFG): Defines the syntax rules of the language.
- Parse Tree: Represents the structure of the program.
- Parsing Techniques: Methods to analyze and process tokens.
- Error Handling: Detects and recovers from syntax errors.
Context-Free Grammar (CFG)
A context-free grammar (CFG) defines the rules for valid syntax in a programming language. It consists of:
- Non-terminals (N): High-level structures like expressions, statements.
- Terminals (T): Actual symbols in the language (e.g., keywords, operators).
- Production Rules (P): Rules that define how terminals and non-terminals combine.
- Start Symbol (S): The highest-level construct in the grammar.
CFG provides a structured approach to define the syntax of a language.
Parse Tree
A parse tree is a tree representation of how an input follows the grammar rules.
Example for expression 3 + 4 * 5:
.
+
/ \
3 *
/ \
4 5
Parsing Techniques
Parsers analyze tokens using different techniques:
- Top-Down Parsing: Starts from the root and derives the input.
- Bottom-Up Parsing: Starts from input tokens and builds up.
Error Handling in Syntax Analysis
Syntax analysis also involves detecting and handling errors.
- Panic Mode Recovery: Skips invalid tokens until a valid construct is found.
- Phrase-Level Recovery: Inserts or deletes tokens to correct errors.
Steps in Syntax Analysis
Syntax analysis follows a structured approach to process tokens and check for valid syntax.
Step 1: Token Input
The parser takes a sequence of tokens from the lexical analyzer.
Step 2: Applying Grammar Rules
The parser attempts to match token sequences to production rules in the grammar.
Step 3: Constructing the Parse Tree
If the tokens match a valid rule, a parse tree is generated.
Step 4: Error Handling
If an invalid sequence is encountered, the parser reports a syntax error and attempts to recover.
Context-Free Grammars (CFGs)
Context-Free Grammar (CFG) is a formal system used to describe the syntax of programming languages. It defines how valid statements and expressions are formed by breaking them into smaller components using a set of production rules.
Why CFG is Important in Syntax Analysis
- CFG provides a structured representation of language syntax.
- Used by parsers to construct syntax trees.
- Ensures syntax correctness before semantic analysis.
- Helps in error detection and recovery.
Components of a CFG
A CFG is formally defined as a 4-tuple: G = (N, T, P, S), where:
- Terminals (T): Actual symbols from the language (e.g.,
if,+,identifier). - Non-terminals (N): Abstract symbols that represent groups of syntactic structures (e.g.,
Expression,Statement). - Start Symbol (S): The root of the derivation (e.g.,
Program), from which parsing begins. - Production Rules (P): A set of transformation rules defining how non-terminals expand into terminals and other non-terminals.
Example Production Rules
Consider a simple arithmetic expression grammar:
E → E + T | E - T | T
T → T * F | T / F | F
F → ( E ) | id
Explanation of Components
E(Expression): Represents an entire arithmetic expression.T(Term): Represents multiplication/division operations.F(Factor): Represents atomic values (identifiers or parenthesized expressions).
Example of a CFG for Arithmetic Expressions
The following derivation shows how CFG expands an arithmetic expression.
Example Expression:
3 + 4 * (5 - 2)
Step-by-Step Derivation:
E → E + T
→ T + T
→ F + T
→ 3 + T
→ 3 + T * F
→ 3 + F * F
→ 3 + 4 * (E)
→ 3 + 4 * (E - T)
→ 3 + 4 * (F - T)
→ 3 + 4 * (5 - 2)
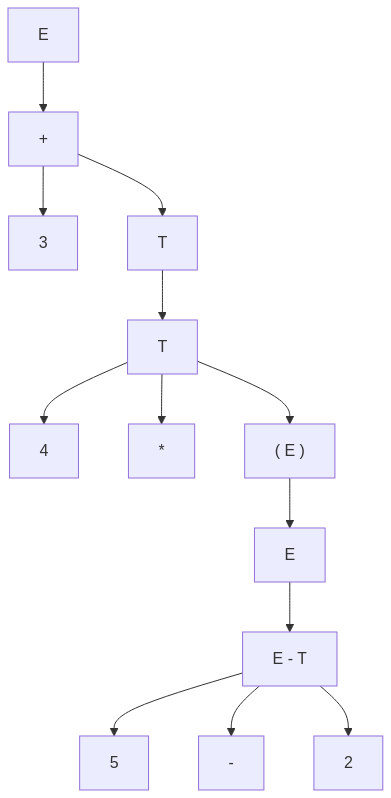
Parse Tree Representation:
graph TD;
E --> E1["+"] --> T1["3"];
E1 --> T2["T"];
T2 --> T3["T"] --> F2["4"];
T3 --> Op["*"];
T3 --> F3["( E )"];
F3 --> E2["E"];
E2 --> E3["E - T"];
E3 --> F4["5"];
E3 --> Op2["-"];
E3 --> T4["2"];
Properties of Context-Free Grammars
- Recursion: CFGs allow recursive definitions, enabling nested expressions (e.g.,
(5 - 2)inside4 * (5 - 2)). - Ambiguity: Some CFGs allow multiple parse trees for the same input.
- Chomsky Hierarchy: CFGs belong to Type-2 grammars, which are more expressive than regular grammars but less than context-sensitive grammars.
Eliminating Ambiguity in CFG
An ambiguous grammar can generate multiple valid parse trees. To resolve this, we modify the rules to enforce precedence and associativity.
Ambiguous Grammar
E → E + E | E * E | id
This grammar allows multiple ways to derive 2 + 3 * 4, causing ambiguity.
Unambiguous Grammar
To enforce correct precedence, we rewrite it as:
E → E + T | T
T → T * F | F
F → id
Now, 3 + 4 * 5 is always parsed as 3 + (4 * 5).
Industry Applications of CFG
- Programming Languages: CFGs define syntax rules in compilers like GCC, Clang, and Java Compiler.
- SQL Parsing: Databases like MySQL and PostgreSQL use CFGs to process SQL queries.
- Natural Language Processing (NLP): Used in chatbots and AI assistants (e.g., Siri, Alexa).
- Code Formatting & Linting: Tools like Prettier, ESLint, and ClangFormat use CFGs for syntax checking.
Parsing Techniques
Parsing techniques are methods used by the syntax analyzer to verify whether a sequence of tokens follows the syntactic rules of a programming language. They determine how the compiler interprets source code and builds syntax trees.
Classification of Parsing Techniques
Parsing techniques are categorized into two major types:
- Top-Down Parsing: Starts from the root of the parse tree and expands using leftmost derivations.
- Bottom-Up Parsing: Starts from the input tokens and gradually reduces them to the start symbol using rightmost derivations.
LL(1) Parsing (Top-Down Parsing)
LL(1) parsing is a predictive parsing technique that scans input from Left to right (L), produces Leftmost derivations (L), and uses 1-token lookahead (1).
Characteristics of LL(1) Parsing
- Requires a predictive parsing table to decide the next step.
- Does not require backtracking (if the grammar is LL(1) compliant).
- Used in recursive descent parsers.
- Efficient for simple, non-ambiguous grammars.
Example Grammar for LL(1) Parsing
E → T E'
E' → + T E' | ε
T → F T'
T' → * F T' | ε
F → ( E ) | id
Parsing Table for LL(1)
| Non-Terminal | Token: id | Token: ( | Token: + | Token: * | Token: ) | Token: $ |
|---|---|---|---|---|---|---|
| E | T E' | T E' | ||||
| E' | + T E' | ε | ε | |||
| T | F T' | F T' | ||||
| T' | ε | * F T' | ε | ε | ||
| F | id | ( E ) |
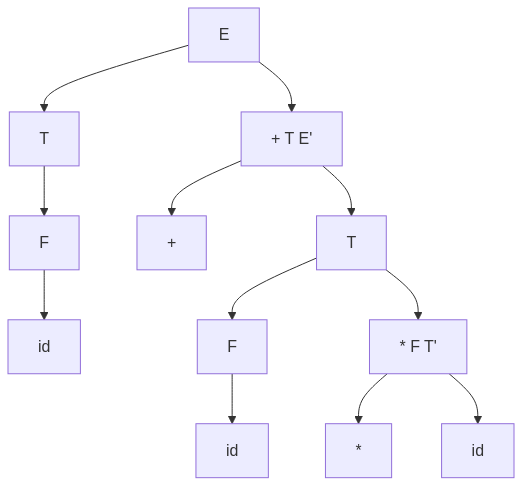
Example LL(1) Parsing of "id + id * id"
graph TD;
Start["E"]
Start --> T["T"]
T --> F["F"]
F --> id["id"]
Start --> E'["\+ T E'"]
E' --> Plus["\+"]
E' --> T2["T"]
T2 --> F2["F"]
F2 --> id2["id"]
T2 --> T'["\* F T'"]
T' --> Mul["\*"]
T' --> F3["id"]
Industry Applications
- ANTLR & JavaCC: Use LL-based parsing for Java and scripting languages.
- JSON Parsers: Many JSON parsers use LL(1) recursive descent.
- Compilers for Simple Languages: Pascal, Basic, and Lisp-based compilers use LL parsers.
LR(1) Parsing (Bottom-Up Parsing)
LR(1) parsing is a shift-reduce parsing technique that scans input from Left to right (L), produces Rightmost derivations (R), and uses 1-token lookahead (1).
Characteristics of LR(1) Parsing
- More powerful than LL(1) (can handle a larger class of grammars).
- Constructs parse trees in a bottom-up manner.
- Used in many modern compilers (GCC, JavaCC, Yacc, Bison).
- Requires an LR parsing table to determine shift/reduce operations.
Example Grammar for LR(1) Parsing
E → E + T | T
T → T * F | F
F → ( E ) | id
Shift-Reduce Parsing Example
For input: id + id * id
| Stack | Input | Action |
|---|---|---|
| [] | id + id * id | Shift |
| [id] | + id * id | Reduce F → id |
| [F] | + id * id | Reduce T → F |
| [T] | + id * id | Shift |
| [T +] | id * id | Shift |
| [T + id] | * id | Reduce F → id |
| [T + F] | * id | Reduce T → F |
| [T + T] | * id | Shift |
| [T + T *] | id | Shift |
| [T + T * id] | Reduce F → id | |
| [T + T * F] | Reduce T → T * F | |
| [T + T] | Reduce E → E + T |
Industry Applications
- GCC & Clang: Use LR parsing for efficient C/C++ compilation.
- SQL Query Processors: PostgreSQL and MySQL use LR-based parsing.
- Yacc & Bison: Use LR parsing for generating parsers.
Recursive Descent Parsing
Recursive descent parsing is a top-down technique where each non-terminal is implemented as a recursive function.
Characteristics of Recursive Descent Parsing
- Manually implemented using recursive functions.
- Can be used only for LL(1) grammars.
- Suffers from left recursion issues (must be rewritten to avoid infinite recursion).
- Easy to implement and debug manually.
Example Recursive Descent Implementation
Grammar:
E → T E'
E' → + T E' | ε
T → F
F → id | ( E )
Recursive descent implementation in Python:
def E():
T()
E_prime()
def E_prime():
if lookahead == '+':
match('+')
T()
E_prime()
def T():
F()
def F():
if lookahead == 'id':
match('id')
elif lookahead == '(':
match('(')
E()
match(')')
Industry Applications
- JSON Parsers: Use recursive descent for parsing hierarchical structures.
- Custom Scripting Languages: Many domain-specific languages (DSLs) use it.
Abstract Syntax Trees (ASTs)
An Abstract Syntax Tree (AST) is a hierarchical, tree-like representation of a program’s structure. Unlike a parse tree, which strictly follows grammar rules, an AST provides a condensed and meaningful representation that is closer to execution logic.
Importance of AST in Compilation
- Eliminates redundant syntactic information from parse trees.
- Provides a structured representation for later phases (semantic analysis, optimization, and code generation).
- Enhances compiler efficiency by simplifying operations on the code.
- AST nodes directly map to operations (e.g., expressions, assignments, function calls).
Differences Between Parse Tree and AST
| Feature | Parse Tree | AST |
|---|---|---|
| Represents | Entire grammar structure | Essential syntax for computation |
| Size | Larger (includes all grammar rules) | Smaller (removes unnecessary nodes) |
| Usability | Not suitable for code generation | Used in semantic analysis & optimization |
| Example Usage | Syntax checking | Code optimization, execution |
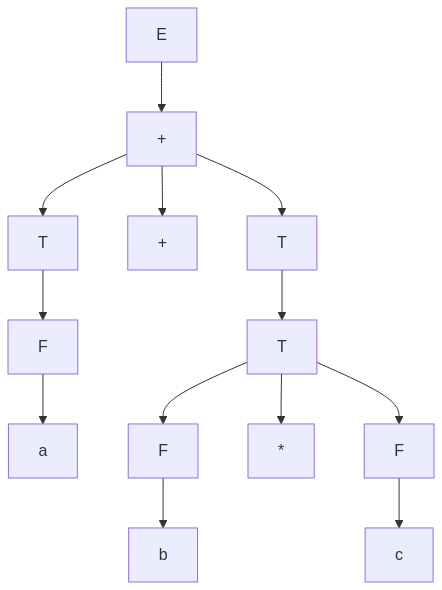
Example: Parse Tree vs. AST for "a + b * c"
Parse Tree:
graph TD;
E["E"]
E --> E1["\+"] --> T1["T"]
E1 --> plus["\+"]
E1 --> T2["T"]
T1 --> F1["F"]
F1 --> a["a"]
T2 --> T3["T"] --> F2["F"]
F2 --> b["b"]
T3 --> mult["\*"]
T3 --> F3["F"]
F3 --> c["c"]
Abstract Syntax Tree (AST):
graph TD;
plus["\+"] --> a;
plus["\+"] --> mult["*"];
mult["\*"] --> b;
mult["\*"] --> c;
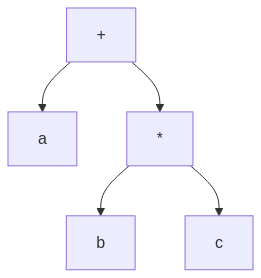
Observations:
- The AST removes unnecessary non-terminal nodes (like E, T, and F).
- It retains only essential operations (addition and multiplication).
- AST directly represents the logical execution order.
Construction of AST
ASTs are constructed using postfix traversal of the parse tree:
- Operators become internal nodes.
- Operands (variables, literals) become leaf nodes.
- Parentheses do not appear in ASTs as precedence is inherently maintained.
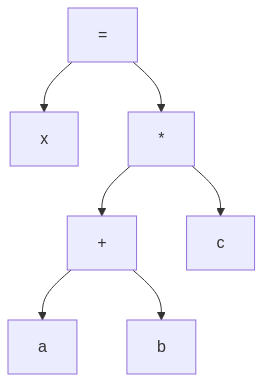
Example: AST Construction for "x = (a + b) * c"
graph TD;
assign["\="] --> x;
assign["\="] --> mult["\*"];
mult["\*"] --> plus["\+"];
plus["\+"] --> a;
plus["\+"] --> b;
mult["\*"] --> c;
Industry Applications of AST
- Compilers (GCC, Clang, Java Compiler): Use AST for semantic analysis, optimization, and code generation.
- Interpreters (Python, JavaScript Engines): Convert source code into ASTs for execution.
- Static Analysis Tools (ESLint, PyLint): Use ASTs to detect code smells, security vulnerabilities, and optimizations.
- Integrated Development Environments (IDEs): Use ASTs for code refactoring, syntax highlighting, and auto-completion.
Optimizations Using AST
Modern compilers apply optimization techniques on ASTs before generating machine code.
Constant Folding
Computes constant expressions at compile time.
// Original code
x = 5 + 3 * 2;
// Optimized AST
x = 5 + 6;
x = 11;
Dead Code Elimination
Removes unreachable or redundant code.
if (false) { x = 10; } // Eliminated at AST stage
Common Subexpression Elimination
Reuses computed expressions to save execution time.
y = (a + b) * c;
z = (a + b) * d;
After AST optimization:
temp = a + b;
y = temp * c;
z = temp * d;
AST-Based Code Generation
Once the AST is built and optimized, the compiler translates it into low-level code (assembly, bytecode, or machine code).
Example: Converting AST to Assembly
// Expression: a + b * c
mov R1, b
mul R1, c
add R1, a
Tools for AST Manipulation
- LLVM: Uses AST for optimizing code before converting it into machine code.
- ANTLR: Generates ASTs from grammar definitions.
- AST Explorer: Visualizes ASTs for JavaScript and other languages.
- Clang AST Matcher: Allows AST-based source code transformation.
CFG Example and Derivation Analysis
Consider the following Context-Free Grammar (CFG) for arithmetic expressions:
Notations Used
- CFG Notation: A Context-Free Grammar (CFG) is denoted as:
$$ G = (N, T, P, S) $$
where:
- N (Non-terminals): {E, T, F}
- T (Terminals): {id, +, *}
- P (Production Rules): Defined below.
- S (Start Symbol): E
- Derivation Notation:
- Left-most derivation: Expands the leftmost non-terminal first.
- Right-most derivation: Expands the rightmost non-terminal first.
- $\Rightarrow$ means one-step derivation.
- $\Rightarrow^*$ means zero or more steps derivation.
Context-Free Grammar
We define the following CFG:
E → E + E | E * E | ( E ) | id
For the input string:
id + id * id
Parse Trees
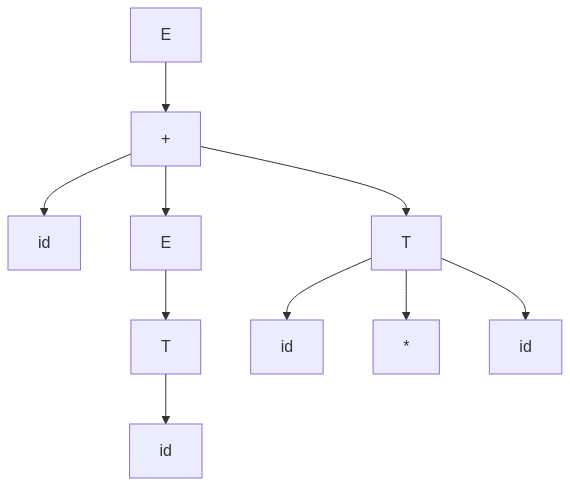
The following parse trees illustrate different ways to derive id + id * id.
Parse Tree 1 (Addition First)
graph TD;
E --> E1["\+"] --> T1["id"];
E1 --> E2["E"];
E2 --> T2["T"];
T2 --> F["id"];
E1 --> T3["T"];
T3 --> F2["id"];
T3 --> Op["\*"];
T3 --> F3["id"];
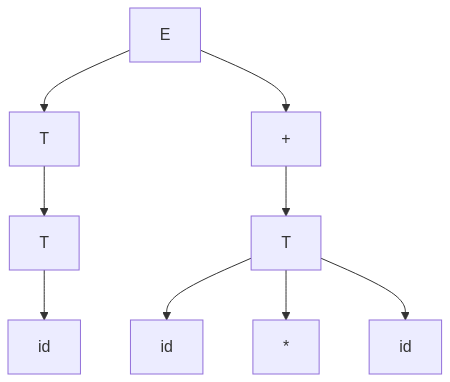
Parse Tree 2 (Multiplication First)
graph TD;
E --> E1["T"];
E1 --> T1["T"];
T1 --> F1["id"];
E --> Op["\+"] --> T2["T"];
T2 --> F2["id"];
T2 --> Op2["\*"];
T2 --> F3["id"];
Left-Most Derivation
A left-most derivation expands the leftmost non-terminal first at each step.
E → E + E
→ id + E
→ id + E * E
→ id + id * E
→ id + id * id
Each step replaces the leftmost non-terminal with one of its production rules.
Right-Most Derivation
A right-most derivation expands the rightmost non-terminal first.
E → E + E
→ E + E * E
→ E + E * id
→ E + id * id
→ id + id * id
Each step replaces the rightmost non-terminal with one of its production rules.
Associativity and Precedence
Click to read the concept in detail
Associativity
- Operators like `+` and `*` are left-associative in most languages.
- For example, `a - b - c` is interpreted as `(a - b) - c`.
- Thus, `id + id * id` should be parsed as:
id + (id * id)Operator Precedence
- Multiplication (`*`) has higher precedence than addition (`+`).
- This means that `id + id * id` should be evaluated as:
id + (id * id)Ambiguous or Unambiguous?
A grammar is ambiguous if the same input has multiple valid parse trees.
- In our case, two parse trees exist:
- One where addition happens first.
- One where multiplication happens first.
Since multiple valid trees exist, the grammar is ambiguous.
Resolving Ambiguity
To resolve ambiguity, we modify the grammar to define precedence and associativity explicitly.
E → E + T | T
T → T * F | F
F → ( E ) | id
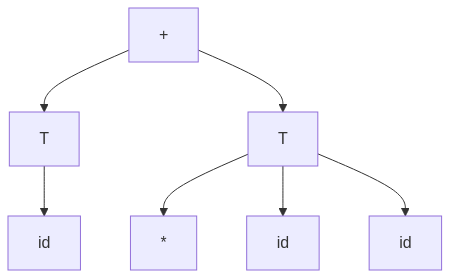
Unambiguous Parse Tree
graph TD;
E["\+"] --> T1["T"];
E["\+"] --> T2["T"];
T1 --> F1["id"];
T2 --> Op["\*"];
T2 --> F2["id"];
T2 --> F3["id"];
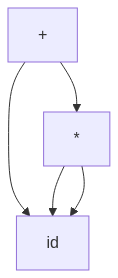
AST Representation
AST (Abstract Syntax Tree) simplifies the parse tree by removing redundant grammar rules.
graph TD;
plus["\+"] --> id;
plus["\+"] --> mult["\*"];
mult["\*"] --> id;
mult["\*"] --> id;
Quick Summary
- Left-most derivation expands left-most symbols first.
- Right-most derivation expands right-most symbols first.
- Operator precedence ensures `id + id * id` is parsed as `id + (id * id)`.
- Left-associativity dictates `a - b - c` is parsed as `(a - b) - c`.
- The original grammar is ambiguous because two different parse trees exist.
- The modified grammar fixes ambiguity by explicitly defining precedence rules.
- Abstract Syntax Tree (AST) eliminates unnecessary nodes, keeping only essential computations.
Real-World Applications of Syntax Analysis (Parser)
Syntax analysis plays a crucial role in real-world applications beyond compiler design. It is widely used in integrated development environments (IDEs), database systems, and various tools that require structured text processing.
Code Validation in IDEs (Auto-Complete, Syntax Errors)
Modern IDEs rely on parsers to validate source code, detect syntax errors, and provide real-time assistance through auto-completion and error highlighting.
How Syntax Analysis Helps in IDEs
- Real-time Syntax Checking: The parser continuously scans and validates code as the user types.
- Auto-Completion: The parser predicts keywords, function names, and variable names based on grammar rules.
- Code Formatting: Properly indents and structures code using parsing techniques.
- IntelliSense & Suggestions: Based on AST analysis, IDEs provide suggestions for function calls, method parameters, and variable names.
Examples of IDEs Using Syntax Analysis
- Visual Studio Code: Uses Language Server Protocol (LSP) to provide syntax analysis for multiple languages.
- JetBrains IntelliJ IDEA: Uses real-time syntax parsing for Java, Kotlin, Python, and more.
- PyCharm: Parses Python code to provide auto-fixes and refactoring suggestions.
Example: Syntax Error Detection in Python
Consider this Python code with a syntax error:
def greet(name)
print("Hello, " + name + "!")
The parser will generate an error:
SyntaxError: expected ':'
The missing colon (:) is detected by the parser before execution.
Auto-Completion Example
When typing:
System.out.pri
The parser suggests:
System.out.print
System.out.println
SQL Query Parsing in Databases
Databases use syntax analysis to parse SQL queries and verify their correctness before execution.
Why SQL Query Parsing is Important
- Ensures syntactic correctness: Prevents malformed queries from executing.
- Optimizes execution plans: The parser helps generate efficient query plans.
- Prevents SQL injection attacks: Structured parsing avoids executing malicious inputs.
Example of SQL Query Parsing
Consider the following SQL query:
SELECT name age FROM users WHERE id = 10;
The parser detects a missing comma:
SyntaxError: Expected ',' between column names
Database Systems Using SQL Parsing
- MySQL: Uses a recursive descent parser to process SQL queries.
- PostgreSQL: Implements bottom-up parsing techniques.
- Oracle Database: Uses LL and LR parsing for advanced SQL features.
Query Optimization
After parsing, SQL databases optimize queries:
- Rearrange joins and conditions for faster execution.
- Use indices and caching to improve efficiency.
- Detect redundant computations to eliminate unnecessary processing.
Other Real-World Applications
- Web Browsers: Parse HTML, CSS, and JavaScript for rendering.
- Natural Language Processing (NLP): Syntax analysis in AI chatbots.
- Markup Language Processors: XML and JSON parsing in applications.
Common Pitfalls & Debugging
Syntax analysis is a crucial phase in the compilation process, but it comes with several challenges. Ambiguous grammars, errors in recursive descent parsing, and recovering from syntax errors require careful handling to ensure accurate and efficient parsing.
Handling Ambiguous Grammars (e.g., Dangling Else)
Ambiguous grammars allow multiple parse trees for a single input, leading to uncertainty in parsing. One common example is the dangling else problem.
Dangling Else Problem
Consider the following ambiguous grammar for conditional statements:
Stmt → if Expr then Stmt | if Expr then Stmt else Stmt | other
Given this input:
if (x > 0)
if (y > 0)
print("Both positive");
else
print("x is negative");
The ambiguity arises because the else statement could belong to either the inner or outer if.
Solution: Using Grammar Rules
- Explicit Block Structuring: Require braces
{}to remove ambiguity. - Associate Else with the Closest If: Many languages adopt this strategy.
- Use Parsing Constraints: Define an unambiguous grammar like:
Stmt → MatchedStmt | UnmatchedStmt
MatchedStmt → if Expr then MatchedStmt else MatchedStmt | other
UnmatchedStmt → if Expr then Stmt | if Expr then MatchedStmt else UnmatchedStmt
Debugging Ambiguous Grammars
- Use Parse Trees: Visualize possible trees for clarity.
- Test with Different Inputs: See how different structures affect parsing.
- Modify Grammar: Introduce non-terminals to enforce precedence.
Debugging Recursive Descent Parser Errors
Recursive descent parsers are easy to implement but can face infinite recursion, backtracking inefficiencies, and left recursion issues.
Common Errors in Recursive Descent Parsing
- Left Recursion: Causes infinite recursion.
- Backtracking Overhead: Inefficient parsing of complex grammars.
- Incorrect Lookahead: Misinterpreting token sequences.
Example: Left Recursion Issue
Consider the left-recursive grammar:
E → E + T | T
T → int | (E)
The recursive descent parser for E would never terminate, as it always calls itself first.
Solution: Convert to Right Recursion
Rewrite the grammar to remove left recursion:
E → T E'
E' → + T E' | ε
T → int | (E)
Now, parsing avoids infinite recursion.
Debugging Recursive Descent Parsers
- Check for Left Recursion: Modify rules to remove direct recursion.
- Use Logging: Print debug statements during parsing.
- Restrict Lookahead: Ensure 1-token lookahead is sufficient.
- Trace Execution Flow: Identify excessive backtracking.
Recovering from Syntax Errors Effectively
A syntax error occurs when the source code does not follow the grammar rules. A good parser should handle errors gracefully without stopping compilation.
Types of Syntax Errors
- Missing Tokens: Forgetting semicolons, parentheses.
- Misplaced Tokens: Incorrect order of keywords.
- Unexpected Tokens: Extraneous symbols in expressions.
Error Recovery Strategies
Panic Mode Recovery
Immediately discards tokens until a known synchronizing token is found (e.g., semicolon, closing brace).
- Example: If a missing semicolon is detected, skip tokens until the next statement.
- Use Case: Works well for unexpected tokens.
Phrase-Level Recovery
Attempts to replace incorrect tokens with plausible alternatives.
- Example: If
int x 5;is found, replace5with= 5. - Use Case: Useful for minor syntax mistakes.
Error Productions
Adds specific rules to handle common errors.
- Example: If an
elseappears without anif, issue a warning. - Use Case: Helps handle recurring mistakes.
Global Correction
Uses sophisticated algorithms to suggest corrections.
- Example: IDEs suggest fixes for missing tokens.
- Use Case: Advanced compilers like Clang and GCC.
Example: Syntax Error Handling in C
Consider the erroneous code:
int main() {
printf("Hello World")
}
The parser detects:
SyntaxError: Expected ';' after printf statement.
Industry Applications of Debugging Techniques
- Compilers (GCC, Clang): Use syntax recovery strategies.
- IDEs (VS Code, IntelliJ): Suggest corrections via error recovery.
- Web Browsers: JavaScript parsers handle missing braces.
- Database Systems: SQL parsers recover from missing keywords.
Advanced Optimization for Industry Use
Modern compilers employ advanced optimization techniques in syntax analysis to ensure efficient parsing, reduced ambiguity, and improved performance. The following methods—associativity, operator precedence parsing, and lookahead parsing—are widely used in industry-grade parsers.
Associativity
Associativity determines how operators of the same precedence are grouped in an expression. This rule prevents ambiguity and ensures consistent evaluation.
Types of Associativity
- Left-Associative Operators: Operators that group from left to right.
- Right-Associative Operators: Operators that group from right to left.
- Non-Associative Operators: Operators that cannot be chained.
Examples of Associativity
Left-Associative Operators:
These operators evaluate from left to right.
a - b - c // Evaluated as (a - b) - c
a / b / c // Evaluated as (a / b) / c
Right-Associative Operators:
These operators evaluate from right to left.
a = b = c // Evaluated as a = (b = c)
x ^ y ^ z // In some languages, exponentiation is right-associative
Non-Associative Operators:
These operators cannot be chained together.
a < b < c // Syntax error in some languages
Implementing Associativity in Parsing
Associativity rules are enforced in parsing tables and Abstract Syntax Trees (ASTs).
- For left-associative operators, the parser reduces expressions as soon as possible.
- For right-associative operators, the parser defers reduction until all operands are read.
Industry Applications
- Python & JavaScript: Use right-associativity for assignment operators.
- GCC & Clang: Define operator rules in syntax parsing tables.
- Database Query Engines: Apply associativity rules in SQL parsing.
Operator Precedence Parsing
Operator precedence parsing ensures correct evaluation order for mathematical and logical expressions.
Why Operator Precedence Matters
- Operators must be evaluated in the correct order without ambiguity.
- Parsing efficiency improves when precedence rules are encoded in the parser.
- Reduces the need for parentheses in expressions.
Example: Incorrect vs. Correct Precedence
// Without precedence, this is ambiguous:
x = 5 + 3 * 2 // Should be x = 5 + (3 * 2), not (5 + 3) * 2
Operator Precedence Table
Compilers use a precedence table to resolve expression parsing:
| Operator | Associativity | Precedence |
|---|---|---|
* / % |
Left | 3 |
+ - |
Left | 2 |
= |
Right | 1 |
Implementing Operator Precedence Parsing
Operator precedence parsing uses shift-reduce parsing, where:
- Shift: Read the next token (if it has higher precedence).
- Reduce: Apply an operator rule when precedence dictates.
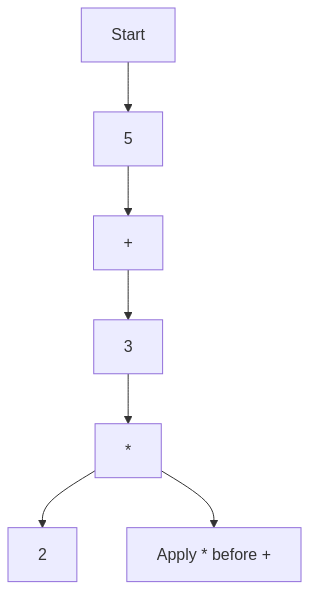
Example: Parsing "5 + 3 * 2"
graph TD;
Start --> Num1[5]
Num1 --> Op1[+]
Op1 --> Num2[3]
Num2 --> Op2[*]
Op2 --> Num3[2]
Op2 --> Reduce[Apply * before +]
Industry Applications
- Compilers (GCC, Clang): Implement operator precedence rules in parser tables.
- Mathematical Computation Tools (MATLAB, Wolfram Alpha): Use precedence parsing for expression evaluation.
- Database Systems (MySQL, PostgreSQL): Parse SQL expressions based on precedence rules.
Lookahead Parsing for Predictive Syntax Trees
Lookahead parsing improves efficiency by predicting which rule to apply next without backtracking.
Why Lookahead Parsing is Important
- Reduces ambiguity in LL and LR parsing.
- Eliminates unnecessary backtracking.
- Speeds up parsing in large codebases.
Types of Lookahead Parsing
- LL(1) Parsing: Uses a single token lookahead.
- LR(1) Parsing: Uses a single token lookahead but supports bottom-up parsing.
- LL(k) Parsing: Uses multiple tokens lookahead for complex grammars.
Example: Lookahead in LL(1) Parsing
Consider the grammar:
Stmt → if Expr then Stmt | while Expr do Stmt | other
With lookahead parsing:
- If the next token is "if", apply
if Expr then Stmt. - If the next token is "while", apply
while Expr do Stmt.
Lookahead Parsing Example in a Predictive Parser
For the input:
if (x > 0) then print("Positive");
The parser makes decisions without backtracking:
graph TD;
Start --> Lookahead["Lookahead Token: if"]
Lookahead --> MatchIf["Match: if"]
MatchIf --> Expr["Parse Expression (x > 0)"]
Expr --> MatchThen["Match: then"]
MatchThen --> PrintStmt["Parse Print Statement"]

Industry Applications
- JavaScript Engines (V8, SpiderMonkey): Use LL(1) predictive parsing.
- SQL Query Optimizers: Implement lookahead parsing for fast execution plans.
- GCC and Clang: Use lookahead in LR(1) parsers.